2. Kracht en beweging

2.1 Versnelling en kracht

• Om de snelheid van een voorwerp te veranderen is kracht nodig
• Hoe groter de massa van een voorwerp, hoe meer kracht er nodig is om deze af te remmen

Tweede wet van Newton

Tweede wet van Newton

$F_{res}=m\cdot a$

Hierin is:

• $F_{res}$ de resulterende kracht in Newton ($\mathrm{N}$);
• $m$ de massa van het voorwerp dat versnelt in kilogram ($\mathrm{kg}$);
• $a$ de versnelling in meter per seconde kwadraat ($\mathrm{m}{\mathrm{s}}^{-2}$).

Traagheid: hoe gemakkelijk of hoe moeilijk je de snelheid van het voorwerp kunt veranderen. Dit is dus iets anders dan snelheid.

Zwaartekracht

Zwaartekracht

$F_z=m\cdot g=m\cdot 9.81\mathrm{N}\cdot \mathrm{k}{\mathrm{g}}^{-1}$

Hierin is:

• $m$ de massa in kilogram ($\mathrm{kg}$);
• $g$ de zwaartekrachtconstante in newton per kilogram ($\mathrm{N}\cdot \mathrm{k}{\mathrm{g}}^{-1}$).

$g$ is dus een versnelling en wordt de valversnelling genoemd.

Luchtweerstandskracht

Luchtweerstandskracht

$F_{w,l}=\frac{1}{2}\cdot C_w\cdot \rho \cdot A\cdot v^2$

Hierin is:

• $F_{w,l}$ de luchtweerstandskracht in newton ($\mathrm{N}$);
• $C_w$ de wrijvingscoëfficiënt (geen eenheid);
• $\rho$ de dichtheid van de lucht in kilogram per kubieke meter ($\mathrm{kg}\cdot {\mathrm{m}}^{-3}$);
• $A$ het frontale oppervlak in vierkante meter (${\mathrm{m}}^2$); dit is het oppervlak dat je van voren ziet;
• $v$ de snelheid van het voorwerp ten opzichte van de lucht in meter per seconde ($\mathrm{m}\cdot {\mathrm{s}}^{-1}$).

2.2 Krachten samenstellen

Resulterende kracht, resultante: het netto-effect van alle krachten op een voorwerp. Alle krachten (als vectoren) bij elkaar opgeteld, het resultaat is een nieuwe vectorgrootheid, die aangeeft waar het voorwerp heen gaat.

Grootheden

Op dit moment zijn er twee soorten grootheden belangrijk:

1. Vectorgrootheden

1. Vectorgrootheden; elke vectorgrootheid heeft:
   • een grootte (de lengte van de vector);
   • een richting;
   • een beginpunt of aangrijpingspunt, de zwaartekracht grijpt altijd aan in het zwaartepunt van een massa.
2. Scalaire grootheden: grootheden die alleen een grootte hebben en geen richting.

Deze twee grootheden houden we uit elkaar door boven een vectorgrootheid een pijltje te zetten: $\vec{F}$. Als je alleen de grootte van een vectorgrootheid wilt aangeven, dan laat je het pijltje weg: $F$.

Vectoren samenstellen

Er zijn meerdere manier om vectoren samen te stellen. Omdat vectoren op een andere manier optellen dan getallen (scalairen) spreken we van samenstellen.

Het is bij het tekenen van vectoren altijd nodig om een schaal te vermelden! $20\mathrm{N}$ is tenslotte geen lengtemaat.

Kop-staartmethode

Bij deze methode teken je alle vectoren en verplaats je deze zodat ze elk de achterkant van één andere vector raken. Je tekent nu een lijn vanuit het begin van deze slinger (het aangrijpingspunt) en deze lijn eindigt bij het uiteinde van de slinger. Deze nieuwe lijn is ook een vector en het resultaat van het optellen.

Parallellogram methode

Deze methode lijkt veel op de kop-staartmethode, alleen werkt deze maar voor maximaal 2 vectoren. Het voordeel is echter dat de parallellogram methode over het algemeen precieser is.

Teken voor elke vector een parallelle lijn, het kruispunt van deze twee parallellen is het uiteinde van de resulterende vector. Teken nu dus een lijn vanuit het aangrijpingspunt en het einde, dit is het resultaat.

Simpel berekenen (rechte hoek)

Als twee krachten $F_1$ en $F_2$ loodrecht (hoek van $90^{\circ }$) op elkaar staan, dan vormt de resulterende kracht $F_{res}$ de schuine zijde van een rechthoekige driehoek. In dit geval kun je stelling van pythagoras gebruiken om de grootte van de resulterende kracht te berekenen.
$F_{res}=\sqrt{F_1^2+F_1^2}$

Numerieke manier

Als de hoek tussen de vectoren geen $90^{\circ }$ ligt het voor de hand een van de eerste twee manieren gebruiken, hiervoor is het echter nodig de krachten te tekenen. Dit hoeft niet per se, er zijn namelijk ook manieren om vectoren samen te stellen zonder ze te tekenen, dit komt niet op de toets, maar is handig om te weten en zo vectoren beter te leren begrijpen.

Vectoren zijn namelijk weer te geven als een soort coördinaten, ze starten op $(0,0)$ en eindigen op $(x,y)$. Omdat dit geen echte coördinaten zijn, maar vectoren, geven we ze anders weer:
$\vec{A}=\left[\begin{array}{c}{A}_x\\ A_y\end{array}\right],\vec{B}=\left[\begin{array}{c}{B}_x\\ B_y\end{array}\right]$
Twee vectoren optellen wordt nu in eens heel simpel:
$\vec{A}+\vec{B}=\left[\begin{array}{c}{A}_x+B_x\\ A_y+B_y\end{array}\right]$

Resulterende kracht

${\vec{F}}_{res}=\overrightarrow{F_1}+\overrightarrow{F_2}+\cdots ={\sum }_i\overrightarrow{F_i}$

2.3 Krachten ontbinden

Een kracht kan tegelijkertijd meerdere effecten hebben. In twee dimensies zijn er meestal twee componenten, meestal de kracht op de x-as en de kracht op de y-as. Deze hebben beide natuurlijk een ander effect. Om de krachten los te kunnen bekijken, moet je ze eerst ontbinden.

Componenten door constructie bepalen.

Door een kracht in de juiste richten op schaal te tekenen, kun je door constructie de componenten bepalen. Dat doe je als volgt:

1. Teken de kracht op schaal en onder de juiste hoek.
2. Teken vanuit het begin van de pijl lijnen in horizontale en verticale richtin. Dit zijn de richtingen waarin je de component van de kracht wilt weten.
3. Teken vanuit de pijlpunt een horizontale stippellijn tot aan de verticale lijn. Teken ook een verticale stippellijn vanuit de pijlpunt tot aan de horizontale lijn.
4. Teken pijlen vanuit het begin van de kracht tot de snijpunten van de stippellijnen met de horizontale en de verticale lijn.
5. De verticale en horizontale pijlen geven de componenten aan. Met de schaal kun je de lengten omrekenen naar krachtcomponenten.
   

Het is belangrijk om te snappen dat als je de resulterende kracht van de twee componenten bepaalt, je uiteindelijk dezelfde tekening krijgt.

Deze methode werkt ook wanneer de richtingen waarin je de kracht wilt ontbinden onderling niet loodrecht zijn. In dat geval teken je de stippellijnen parallel aan de twee richtingen waarin je de kracht wilt ontbinden. Er vormt een parallelogram en dit heet de paralellogramconstructie.

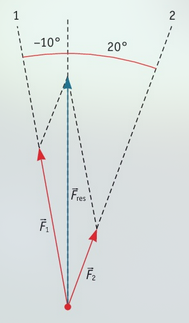
Componenten berekenen

Als de twee richtingen waarin je een kracht ontbindt loodrecht op elkaar staan, kun je de componenten ook berekenen.
De gegeven kracht $F$ is de schuine zijde. De horizontale component $F_x$ is de aanliggende rechthoekszijde (trigonometrie), de verticale component $F_y$ de overstaande rechthoekszijde. De hoek tussen de x-as en de gegeven kracht noemen we $alpha$. Hieruit volgen de volgende formules:
$F_x=F\cdot \cos \alpha$
en
$F_y=F\cdot \sin \alpha$

Massa op een helling berekenen

Een veelvoorkomende situatie is een voorwerp op een helling. De zwaartekracht wijst hierbij natuurlijk naar beneden. Om te berekenen met welke kracht het voorwerp naar beneden gaat, moet de zwaartekracht ontbonden worden.
De component loodrecht op de helling, $F_{z,\perp }$, duwt de slee de sneeuw in. Alleen de component evenwijdig aan de helling, $F_{z,\parallel }$, zorgt ervoor dat de slee in die richting naar beneden zal glijden. In de constructie van de onderstaande figuur zie je dat $F_z$ de shuine zijde van een rechthoekige driehoek is. Je kunt de componenten daarom als volgt berekenen: $F_{z,\perp }=F_z\cdot \cos \alpha$ en $F_{z,\parallel }=F_z\cdot \sin \alpha$

2.4 Krachten in evenwicht

Eerste wet van Newton

De eerste wet van Newton is niet heel spannend. Het is de Tweede wet van Newton, maar dan waarbij $F_{res}=0$. Dit zorgt er natuurlijk voor dat $a=0$, want $F_{res}=0=m\cdot a$. Hieruit kun je het volgende halen:

De eerste wet van Newton

Een voorwerp waarop geen resulterende kracht werkt, versnelt niet. Andersom werkt dit ook: wanneer een voorwerp in rust is of met constante snelheid beweegt, is de resulterende kracht op het voorwerp nul.

Normaalkracht

Volgens de eerste wet van Newton is de resulterende kracht op een boek dat stil op tafel ligt gelijk aan nul. Omdat in ieder geval de zwaartekracht op het boek werkt, moet er nog een andere kracht zijn die het boek op zijn plek hoedt. Die kracht moet worden uitgeoefend door de tafel. Immers: als de tafel er niet is, valt het boek naar beneden.

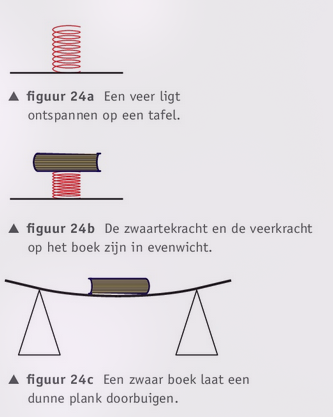
Ook wanneer je het boek op een tafel legt, zal de tafel een klein beetje vervormen en zo de zwaartekracht tegenwerken. Je kunt dus zeggen dat de tafel dan terugduwt. Deze kracht wordt de normaalkracht genoemd, weergegeven met $F_N$. Normaal is een ander woord voor een lijn die loodrecht op een vlak staat. De normaalkracht is namelijk een kracht die altijd loodrecht op het oppervlak staat waarop een voorwerp ligt.

Wet van Hooke

De normaalkracht komt dus tot stand doordat de ondergrond vervormt. Een voorwerp dat kan vervormen, is bijvoorbeeld een veer. Bij een veer wordt de kracht veerkracht genoemd. Als de vervorming niet te groot is, en de veer dus als er geen kracht meer op uitgeoefend wordt gewoon weer naar zijn originele staat terug gaat, dan wordt de veerkracht gegeven door de wet van Hooke.

Wet van Hooke

$F_v=C\cdot u$

Hierin is:

• $F_v$ de op de veer uitgeoefende kracht in newton ($\mathrm{N}$);
• $C$ de veerconstante in newton per meter ($\mathrm{N}\cdot {\mathrm{m}}^{-1}$);
• $u$ de uitrekking of indrukking in meter ($\mathrm{m}$).

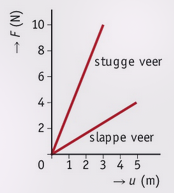
De wet van Hooke is een recht evenredig verband: teken je deze in een diagram vormt er een rechte lijn door de oorsprong. Als je voor een bepaalde veer het verband (de verhouding) tussen $F_v$ en $u$ kent, dan kun je de veer gebruiken als veerunster om krachten mee te meten.

Rol- en luchtweerstand

Voertuigen, zoals fietsen en auto’s, hebben altijd last van twee soorten wrijving: rolweerstand en luchtweerstand. Rolweerstand, $F_{w,t}$, is de tegenwerking die een voorwerp ondervindt door de vervorming van banden en ondergrond. Rolweerstand onstaat dus niet doordat een band over de weg schuift. Het deel van de band dat contact maakt met de grond beweegt namelijk niet ten opzichte van de grond.

Schuifweerstand

Wanneer je een slee over asfalt trekt, merk je dat dit een stuk lastiger gaat dan als je deze over de sneeuw heen trekt. Dit komt doordat asfalt een stuk ruwer is dan de sneeuw en dit zorgt voor weerstand. De weerstand in deze situatie heet schuifweerstand, $F_{w,s}$. Schuifweerstand ontstaat doordat voorwerpen niet perfect glad zijn. Als je het oppervlak van een voorwerp sterk uitvergroot, zie je allemaal oneffenheden, deze grijpen in elkaar. Als je een horizontale kracht uitoefent, dan duw je eigenlijk tegen al die oneffenheden aan. Je moet het voorwerp als het ware een stukje optillen, of de oneffenheden vervormen om het voorwerp in beweging te krijgen.

Schuifweerstand

$F_{w,s,max}=f\cdot F_N$

Hierin is:

• $F_{w,s,max}$ de maximale schuifweerstand in newton ($\mathrm{N}$);
• $f$ de schuifwrijvingscoëfficiënt: een constante (zonder eenheid) die afhangt van de eigenschappen van de ondergrond en het voorwerp. Deze moet experimenteel worden vastgesteld;
• $F_N$ de normaalkracht op het voorwerp in newton ($\mathrm{N}$).