3. Energieomzetting

3.1 Stijgen en dalen

Arbeid in één richting

Arbeid in één richting

$W=F\cdot s$

Hierin is:

• $W$ de arbeid in newtonmeter ($\mathrm{N}\cdot \mathrm{m}$);
• $F$ de kracht in Newton ($\mathrm{N}$);
• $s$ de verplaatsing in meter ($\mathrm{m}$) in dezelfde richting als de kracht $F$.

De eenheid newtonmeter is te vervangen voor de eenheid joule: $1\mathrm{N}\cdot \mathrm{m}=1\mathrm{J}$.

Arbeid bij verticaal hijsen en tillen

Arbeid bij verticaal hijsen en tillen

$W=m\cdot g\cdot h$

Hierin is:

• $W$ de arbeid in newtonmeter ($\mathrm{N}\cdot \mathrm{m}$);
• $m$ de massa van het object in kilogram ($\mathrm{kg}$);
• $g$ de valversnelling in meter per seconde kwadraat ($\mathrm{m}\cdot {\mathrm{s}}^{-2}$);
• $h$ de hoogte tot waar je het object optilt in meter ($\mathrm{m}$).

De formule voor arbeid bij verticaal hijsen en tillen is te beredeneren vanuit de formule voor arbeid in één richting. Op een massa $m$ werkt een zwaartekracht $F_z=m\cdot g$. Wanneer je een massa verticaal omhoog tilt, oefen je een even grote kracht uit dan de zwaartekracht, maar in tegenovergestelde richting.
$W=F\cdot s=F_z\cdot h=m\cdot g\cdot h$

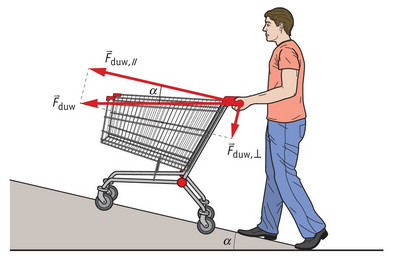
Kracht en verplaatsing niet in dezelfde richting

Kracht en verplaatsing niet in dezelfde richting

$W=F\cdot s\cdot \cos \alpha$

Hierin is:

• $W$ de arbeid in newtonmeter ($\mathrm{N}\cdot \mathrm{m}$);
• $F$ de kracht in Newton ($\mathrm{N}$);
• $s$ de verplaatsing in meter ($\mathrm{m}$) in dezelfde richting als de kracht $F$;
• $\alpha$ de hoek tussen de kracht $F$ en de verplaatsing $s$ .

Dit is gemakkelijk te beredeneren: de kracht wordt ontbonden waarbij een gedeelte in dezelfde richting gaat als de verplaatsing en het andere gedeelte hier loodrecht op. Als de hoek $90°$ is, is de arbeid altijd $0$.

3.2 Starten en stoppen

Belangrijke voorkennis

Er zijn een aantal formules uit het vorige hoofdstuk die handig zijn om het verband tussen arbeid en snelheidsverandering te beredenering:
Het onderstaande geldt als de kracht constant is en het voorwerp versnelt vanuit rust.

• Als op een voorwerp met massa $m$ een constante kracht $F$ werkt, is de versnelling gelijk aan $a=\frac{F}{m}$; dit is de Tweede wet van Newton
• De afgelegde afstand op tijdstip $t$ is $s=\frac{1}{2}\cdot a\cdot t^2$
• De snelheid op tijdstip $t$ is $v=a\cdot t$
• $s=v_{gem}\cdot t$
• $v_{gem}=\frac{1}{2}\cdot v_{eind}$
• $a\cdot t=v_{eind}$

Vanuit rust met constante versnelling

• $W=F\cdot s$
• Met $F=m\cdot a$ en $s=v_{gem}\cdot t$ volgt $W=m\cdot a\cdot v_{gem}\cdot t$
• Omdat $v_{gem}=\frac{1}{2}\cdot v_{eind}$ en $a\cdot t=v_{eind}$ volgt $W=\frac{1}{2}\cdot m\cdot v_{eind}^2$

Als een voorwerp versnelt vanuit rust en de versnelling gelijk blijft geldt dus:
$W=\frac{1}{2}\cdot m\cdot v_{eind}^2$

Een algemenere formule

Er zijn natuurlijk veel gevallen waarin een voorwerp niet versnelt vanuit stilstand en de versnelling niet gelijk blijft. We kunnen de formule hier voor aanpassen.
Deze stappen hoef je niet te kennen, de formule moet je wel kunnen gebruiken.

Bij afremmen is de arbeid negatief, kracht en verplaatsing zijn namelijk tegengesteld gericht. De hoek tussen de richting van de kracht en de richting van de verplaatsing is $\alpha =180°$, de cosinus daarvan is gelijk aan $-1$, waardoor de uitkomst van $W=F\cdot \cos \alpha$ negatief is.

Hieruit volgt dat de algemene formule voor een beweging met een beginsnelheid en een eindsnelheid is:

Theorem

$W=\frac{1}{2}\cdot m\cdot v_{eind}^2-\frac{1}{2}\cdot m\cdot v_{begin}^2$

Hierin is:

• $W$ de arbeid in newtonmeter ($\mathrm{N}\cdot \mathrm{m}$);
• $m$ de massa van het object in kilogram ($\mathrm{kg}$);
• $v_{begin}$ de versnelling van het object aan het begin in meter per seconde ($\mathrm{m}\cdot {\mathrm{s}}^{-1}$);
• $v_{eind}$ de versnelling van het object aan het einde in meter per seconde ($\mathrm{m}\cdot {\mathrm{s}}^{-1}$);

Zie dat wanneer je start vanuit stilstand, het tweede deel van de formule gelijk is aan 0, waardoor je de eerder genoemde formule krijgt.
Wanneer je eindigt in stilstand, is het eerste deel van de formule gelijk aan 0, waardoor je het omgekeerde van de eerste formule krijgt (te beredeneren met $\cos 180°=-1$)

Niet constante snelheid

Uitleg volgt nog
$\Sigma W=\frac{1}{2}\cdot m\cdot v_{eind}^2-\frac{1}{2}\cdot m\cdot v_{begin}^2$

3.3 Spannen en ontspannen

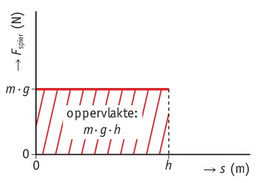
Omdat $W=F\cdot s$, kan je een grafiek waarin de kracht tegen de plaats is afgedrukt om de arbeid te berekenen. Door de oppervlakte onder de grafiek te meten, kom je ook op de arbeid uit. Je kan dus grafisch de arbeid bepalen, zelfs wanneer de kracht verandert als de positie verandert. Voorwaarde is wel dat de kracht $F$ in de richting van de verplaatsing $s$ werkt.

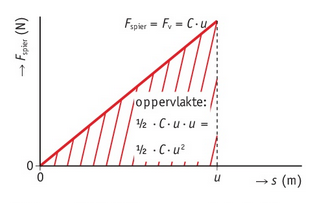
Arbeid uitrekking veer

Een uitrekking bij een voorwerp dat aan de Wet van Hooke voldoet.

Arbeid uitrekking veer

$W=\frac{1}{2}\cdot C\cdot u^2$

Hierin is:

• $W$ de arbeid in newtonmeter ($\mathrm{N}\cdot \mathrm{m}$);
• $C$ de veerconstante in newton per meter ($\mathrm{N}\cdot {\mathrm{m}}^{-1}$);
• $u$ de uitrekking of indrukking in meter ($\mathrm{m}$).

Dit is te beredeneren vanuit $F_v=C\cdot u$. Zetten we de kracht af tegen de uitrekking (verplaatsing), krijgen we de onderstaande grafiek. De bovenstaande formule berekend hierbij de oppervlakte onder de grafiek.

Belangrijk

Als je een veer twee keer zo ver uitrekt, verricht je vier keer zoveel arbeid. Als je een massa twee keer zo hoog op, dan verricht je ook twee keer zo veel arbeid.

3.4 Behoud van energie

Energie gaat nooit verloren, het totaal van de energie bij elkaar opgeteld zal altijd op hetzelfde uitkomen. Als arbeid wordt verricht, wordt de ene energiesoort omgezet in een andere, maar de totale energie blijft constant. Dit principe heet de wet van het behoud van energie.

Er zijn in dit hoofdstuk drie energiesoorten die handig zijn om te kennen, deze heten gezamenlijk mechanische energie, omdat ze allemaal met kracht en beweging te maken hebben:

• De veerenergie die is opgeslagen in een gespannen veer is groter als de uitrekking groter is en als de veer stugger is (dus een grotere veerconstante $C$ heeft). Het aantal opgeslagen joules is gelijk aan het aantal joules arbeid dat je erin moet stoppen om de veer te spannen. Die hoeveelheid is gelijk aan $E_v=\frac{1}{2}\cdot C\cdot u^2$
• De kinetische energie van een voorwerp is groter als de massa groter is en als de snelheid groter is. De arbeid die je moet verrichten om een voorwerp een bepaalde snelheid te geven, laat zien hoeveel joule er in deze energievorm is opgeslagen: $E_k=\frac{1}{2}\cdot m\cdot v^2$. Deze energievorm wordt ook wel bewegingsenergie genoemd.
• Als een voorwerp op een bepaalde hoogte is, heeft het zwaarte-energie. Hoe hoger het voorwerp en hoe groter de massa, hoe meer zwaarte-energie. De hoeveelheid zwaarte-energie is gelijk aan de arbeid die je moet verrichten om het voorwerp naar die hoogte te brengen: $E_z=m\cdot g\cdot h$.

Als er geen energie bij komt (uit bijvoorbeeld brandstof) en er geen energie verloren gaat (bijvoorbeeld in de vorm van warmte), dan is het systeem een gesloten systeem. Daarbinnen is de totale mechanische energie constant.

De zwaarte-energie en de veerenergie zijn allebei voorbeelden van potentiële energie. Dat is een verzamelnaam voor soorten energie die afhangen van de positie van het ene voorwerp ten opzichte van het andere.

Arbeid bij starten en stoppen met een niet constante snelheid

De eerder genoemde formule hiervoor was $\Sigma W=\frac{1}{2}\cdot m\cdot v_{eind}^2-\frac{1}{2}\cdot m\cdot v_{begin}^2$. Nu we weten dat $\frac{1}{2}\cdot m\cdot v^2$ de kinetische energie wordt genoemd kunnen we dit veel simpeler schrijven. De nieuwe formule wordt:

Arbeid bij starten en stoppen met een niet constante snelheid

$\Sigma W=\Delta E_k$

3.5 Energie om arbeid te verrichten

In het dagelijks leven zijn er veel situaties waarbij een object in beweging gebracht moet worden: denk aan een lift of auto. We weten vanwege $\Sigma W=\Delta E_k$ dat dit altijd energie kost. Maar als het totaal aan energie in een systeem altijd gelijk blijft, waar komt deze kinetische energie dan vandaan?

Energie komt (zoals eerder omschreven) voor in meerdere vormen. Deze vormen van energie kunnen naar elkaar worden omgezet, om dit te bereiken is eigenlijk altijd een soort tussenstap nodig.

flowchart LR

A([Chemische energie]) --> B(Motor)

B --> C([Kinetische energie])

flowchart LR

A([Kinetische energie]) --> B(Dynamo)

B --> C([Elektrische energie])

Voorbeeld: Lift

In een lift zit een elektromotor, deze zet elektrische energie (uit het net) om in bewegingsenergie. Het systeem is dus pas gesloten als je de lift en het net samen bekijkt.
De lift werkt op een bepaalde spanning $U$, om de motor te laten draaien (en de lift omhoog te laten gaan) moet er stroom $I$ lopen door de elektromotor. Het elektrisch vermogen is dan $P_{el}=U\cdot I$. Elektrische energie wordt gegeven met $E_{el}=P\cdot t$, door deze twee formules samen te nemen kan je zien dat elektrische energie wordt gegeven met: $E_{el}=U\cdot I\cdot t$.

Voorbeeld: Auto

In een auto met een verbrandingsmotor wordt brandstof verbrand om vooruit te komen. Bij de verbranding wordt een gas verwarmd dat uitzet en de motor in beweging brengt. De brandstof bevat energie die vrijkomt door een chemisch proces: verbranding. De energie die in de brandstof zit, wordt daarom chemische energie genoemd. Deze energie wordt uitgedrukt in de stookwaarde ($r$): de hoeveelheid energie per liter of per kilogram van de brandstof. De chemische energie bereken je als volgt:

Chemische energie

$E_{ch}=r_V\cdot V$
$E_{ch}=r_m\cdot m$

Hierin is:

• $r_V$ de stookwaarde ofwel de hoeveelheid energie per volume brandstof, in joule per kubieke meter ($\mathrm{J}\cdot {\mathrm{m}}^{-3}$);
• $V$ het volume van de vrandstof in kubieke meter (${\mathrm{m}}^3$);
• $r_m$ de stookwaarde ofwel de hoeveelheid energie per massa brandstof, in joule per kilogram ($\mathrm{J}\cdot \mathrm{k}{\mathrm{m}}^{-1}$);
• $m$ de massa van de brandstof in kilogram ($\mathrm{kg}$).

Voorbeeld: Sporter

Een sporter moet vaak veel arbeid kunnen verrichten. Deze energie haalt hij uit voedsel. Ju kunt het lichaam zien als een soort verbrandingsmotor. Het voedsel dat je eet, wordt langzaam verbrand. Als je minder energie verbruikt dan je binnenkrijgt, zul je in gewicht aankomen. Voor sporters is het belangrijk goed op hun voeding te letten om een topprestatie te kunnen leveren. De energie in voedsel wordt uitgedrukt in de eenheid kilojoule ($\mathrm{kJ}$) of kilocalorie ($\mathrm{kcal}$). Één calorie is de hoeveelheid warmte die nodig is om één gram (zuiver) water één graad Celsius in temperatuur te doen stijgen.

3.6 Warmte en rendement

Bij de vorige voorbeelden was de totale energie behouden. Dit lijkt echter niet altijd het geval te zijn, dit komt omdat energie vaak niet in maar één andere vorm wordt omgezet.

Voorbeeld

Neem een regendruppel. Als alle zwaarte-energie van een druppel op $2\mathrm{km}$ hoogte zou worden omgezet in kinetische energie, zou de snelheid vlak voor het neerkomen $200\mathrm{m}{\mathrm{s}}^{-1}$ zijn. Gelukkig kot de druppel met een lagere snelheid op je hoofd. De enorme hoeveelheid zwaarte-energie wordt niet geheel omgezet in kinetische energie.

Warmte meetellen

Vaak begint een proces met energie in de vorm van elektrische energie of chemische energie (in brandstoffen) en zet je deze om in mechanische energie. Alle energiesoorten, die je ‘in het proces’ stopt, moeten worden meegeteld als je de wet van behoud van energie toepast.
Alle energiesoorten die ‘uit het proces komen’ moet je dus ook meetellen. Hoewel in veel gevallen het doen kinetische energie is, komt bij deze processen vaak ook warmte vrij. Dit wordt ook wel stralingsenergie genoemd (zorgt ook voor licht). Als je warmte en stralingsenergie meerekent, dan geldt de wet van behoud van energie nog steeds.

Wet van behoud van energie

$\Sigma E_{in}=\Sigma E_{uit}$

Wrijving door luchtweerstand en rolweerstand

Als er wrijving is, ontstaat er warmte. Een voorbeeld hiervan is luchtweerstand, de wrijving tussen het object en de lucht. Hoe meer luchtweerstand, hoe meer energie er ‘verloren’ gaat in de vorm warmte.

Een andere vorm van wrijving is rolweerstand, hierdoor wordt het rollende object een beetje warm, waardoor er dus energie (onbedoeld) wordt omgezet in warmte.

De energiesoort warmte wordt meestal met een hoofdletter $Q$ aangegeven. Er geldt $Q=F_w\cdot s$. De arbeid die de wrijvingskracht op een object verricht is negatief, doordat de kracht en de verplaatsing tegengesteld gericht zijn.

Als in een auto de motor niet werkt, wordt de auto door de wrijvingskracht afgeremd. Er wordt dan kinetische energie omgezet in warmte. Als de motor wel werkt, zort de negatieve arbeid van de wrijvingskracht ervoor dat de snelheid niet eindeloos blijft toenemen, ondanks de positieve arbeid die de stuwkracht verricht. De chemische energie wordt dan niet omgezet in extra kinetische energie, maar in warmte.

Elektrische weerstand

Ook stroomdraden worden warm, als hier elektrische energie doorheen loopt. In een stroomdraad moet het elektron zich door een rooster van trillende metaalatomen met onregelmatigheden worstelen, hierbij treed elektrische weerstand op.

Dit is hoe een gloeidraad van bijvoorbeeld een broodrooster werkt. De elektrische energie wordt uiteindelijk omgezet in stralingsenergie.

Rendement

In de meeste situaties is vrijkomende warmte ongewenst. Je laat geen automotor draaien met de bedoeling dat deze de lucht verwarmt. Ook de warmte die ontstaat in schakelingen van een computer is ongewenst. Het deel van het geheel dat wel wordt omgezet in de gewenste energievorm, noem je het rendement ($\eta$). De definitie van het rendement is: het percentage van de energie die ergens ingaat ($E_{in}$) dat vrijkomt in de vorm die je wilt hebben. De gewenste vrijkomende energie wordt nuttige energie ($E_{nuttig}$) genoemd.

Rendement berekenen

$\eta =\frac{E_{nutttig}}{E_{in}}\cdot 100\%$

3.7 Vermogen

Een trap oprennen is een grotere prestatie dan dezelfde trap rustig oplopen. Bij het verrichten van arbeid haakt het uit in hoeveel tijd je die arbeid verricht. Dit wordt uitgedrukt door de grootheid vermogen.

Vermogen

Vermogen

$P=\frac{W}{t}$

Hierin is:

• $P$ het vermogen in watt ($\mathrm{W}$);
• $W$ de arbeid in joule ($\mathrm{J}$);
• $t$ de tijd waarin de arbeid wordt geleverd in seconde ($\mathrm{s}$).

Uit deze formule kun je aflezen dat de eenheid watt gelijk is aan joule per seconde: $1\mathrm{W}=1\mathrm{J}\cdot {\mathrm{s}}^{-1}$

Vermogen en rendement

Vermogen komt ook voor bij elektrische energie, dan gaat het over elektrisch vermogen. Om het verschil tussen de soorten vermogen duidelijk te maken, kun je kijken naar het ophijsen van een massa met een elektromotor. Het elektrisch vermogen van de elektromotor bereken je met $P_{el}=U\cdot I$. Dit heet het toegevoerde vermogen, ofwel de energie die de elektromotor per seconde van het elektriciteitsnet of een batterij opneemt. Het resultaat van de elektromotor is dat een massa tot een bepaalde hoogte wordt opgetild. Dit kost arbeid: $W=m\cdot g\cdot h$.

Het vermogen dat daarbij hoort is $P=\frac{W}{t}$. Dit is niet gelijk aan het elektrisch vermogen $P_{el}$.

Een elektromotor gebruikt namelijk niet al het opgenomen vermogen om de massa op te tillen. Een deel van de energie komt vrij als warmte (dat is niet-nuttige energie). Die warmte kun je vaak goed voelen.

Je zou kunnen zeggen dat $P=\frac{W}{t}$ het minimale vermogen is dat een mens of apparaat nodig heeft bij het omzetten van energie. Dit is het nuttig geleverde vermogen wanneer het rendement $100\%$ is. In de praktijk zal het rendement lager zijn. Een deel van het vermogen wordt omgezet in warmte. Eerder heb gelezen hoe je het rendement berekend met energie $E$. Omdat $E=P\cdot t$ kun je het rendement ook uitrekenen met vermogen $P$:
$\eta =\frac{E_{nuttig}}{E_{in}}\cdot 100\%=\frac{P_{nuttig}\cdot t}{P_{in}\cdot t}\cdot 100\%=\frac{P_{nuttig}}{P_{in}}\cdot 100\%$
In het geval van de elektromotor die een massa ophijst, is het nuttig vermogen gelijk aan $P_{nuttig}=\frac{W}{t}$ en het opgenomen vermogen $P_{in}$ gelijk aan $P_{el}=U\cdot I$.

Vermogen en snelheid

Aan het begin heb je gezien dat de arbeid $W$ gedefinieerd is als $W=F\cdot s$. Als je dit invult in de formule voor vermogen, dan krijg je: $P=\frac{W}{t}=\frac{F\cdot s}{t}$. Merk op dat je $\frac{s}{t}$ ook kunt zien als de gemiddelde snelheid. Als je de verplaatsing in een heel korte tijd bekijkt, dan is $\frac{s}{t}$ de snelheid op dat moment. Je kunt het vermogen dus ook als volgt berekenen:

Vermogen en snelheid

$P=F\cdot v$

Hierin is:

• $P$ het vermogen in watt ($\mathrm{W}$);
• $F$ de (gemiddelde) kracht in newton ($\mathrm{N}$);
• $v$ de (gemiddelde) snelheid in meter per seconde ($\mathrm{m}\cdot {\mathrm{s}}^{-1}$)

Dit kun je gebruiken bij het bepalen van het vermogen dat je moet leveren om de luchtwrijving te overwinnen. De luchtweerstandskracht is evenredig met het kwadraat van de snelheid:
$F_{w,l}\sim v^2$
Oftewel $F_{w,l}=k\cdot v^2$ voor een geheel $k$. Het vermogen is dan evenredig met de derde macht van de snelheid:
$P=F_{w,l}\cdot v\sim v^3$
Dus als je twee keer zo hard rijdt, moet je acht keer zoveel vermogen leveren. Het vermogen dat een mens, auto, vliegtuig, trein, enzovoort kan leveren, is vaak een vast gegeven. Het hangt bijvoorbeeld af van hoe fit en getraind je bent. Daarmee ligt bijvoorbeeld ook je maximale snelheid op de fiets vast.

3.9 Energiesoorten

Veerenergie

Veerenergie

$E_v=\frac{1}{2}\cdot C\cdot u^2$

Hierin is:

• $E_v$ de veerenergie in joules ($\mathrm{J}$);
• $C$ de veerconstante in newton per meter ($\mathrm{N}\cdot {\mathrm{m}}^{-1}$);
• $u$ de uitrekking of indrukking in meter ($\mathrm{m}$).

Kinetische energie

Kinetische energie

$E_k=\frac{1}{2}\cdot m\cdot v^2$

Hierin is:

• $E_k$ de kinetische energie in joules ($\mathrm{J}$);
• $m$ de massa van het object in kilogram ($\mathrm{kg}$);
• $v$ de snelheid van het object in meter per seconde ($\mathrm{m}\cdot {\mathrm{s}}^{-1}$).

Zwaarte energie

Zwaarte energie

$E_z=m\cdot g\cdot h$

Hierin is:

• $E_z$ de zwaarte energie in joules ($\mathrm{J}$);
• $m$ de massa van het object in kilogram ($\mathrm{kg}$);
• $g$ de valversnelling in meter per seconde kwadraat ($\mathrm{m}\cdot {\mathrm{s}}^{-2}$);
• $h$ de hoogte van het object in meter ($\mathrm{m}$).

Elektrische energie

Elektrische energie

$E_{el}=P\cdot t=U\cdot I\cdot t$

Hierin is:

• $E_{el}$ de elektrische energie in joules ($\mathrm{J}$);
• $P$ de elektrisch vermogen in watt ($\mathrm{W}$);
• $t$ de tijd in seconden ($\mathrm{s}$);
• $U$ de spanning in volt ($\mathrm{V}$);
• $I$ de stroomsterkte in ampère ($\mathrm{A}$).

Chemische energie

Chemische energie

$E_{ch}=r_V\cdot V$
$E_{ch}=r_m\cdot m$

Hierin is:

• $E_{ch}$ de chemische energie in joules ($\mathrm{J}$);
• $r_V$ de stookwaarde ofwel de hoeveelheid energie per volume brandstof, in joule per kubieke meter ($\mathrm{J}\cdot {\mathrm{m}}^{-3}$);
• $V$ het volume van de brandstof in kubieke meter (${\mathrm{m}}^3$);
• $r_m$ de stookwaarde ofwel de hoeveelheid energie per massa brandstof, in joule per kilogram ($\mathrm{J}\cdot \mathrm{k}{\mathrm{m}}^{-1}$);
• $m$ de massa van de brandstof in kilogram ($\mathrm{kg}$).